Finalidades da Disciplina 

São finalidades desta disciplina de Matemática Aplicada:
- desenvolver a capacidade de usar a Matemática como instrumento de interpretação e intervenção no real;
- desenvolver a capacidade de reconhecer regularidades e modelos matemáticos relevantes em cada aspecto da realidade, e de os utilizar para ajudar a resolver problemas, eventualmente em diálogo com especialistas;
- desenvolver as capacidades de formular e resolver problemas, de comunicar, assim como de memória, de rigor, de espírito crítico e de criatividade;
- utilizar os conhecimentos matemáticos na resolução de problemas, decidindo sobre a razoabilidade de um resultado e sobre o uso, consoante os casos, de cálculo mental, algoritmos de papel e lápis ou instrumentos tecnológicos;
- promover o aprofundamento de uma cultura científica, técnica e humanística que constitua suporte cognitivo e metodológico tanto para a inserção plena na vida profissional como para o prosseguimento de estudos;
- contribuir para uma atitude positiva face à Ciência em geral, reconhecendo o seu papel no progresso e desenvolvimento social e material, ao mesmo tempo que reconhecem a necessidade do desempenho de cada um na manutenção e desenvolvimento dos sistemas; 
- promover a realização pessoal mediante o desenvolvimento de atitudes de autonomia e solidariedade;
- criar capacidades de intervenção social pelo estudo e compreensão de problemas e situações da sociedade actual e, bem assim, pela discussão de sistemas e instâncias de decisão que influenciam a vida dos cidadãos, participando desse modo na formação para uma cidadania activa e participativa.

Programa do Módulo 14- Geometria Circulo

1 Apresentação

O círculo aparece como uma forma geométrica vulgar no património construído, em peças de máquinas com utilidade para funções determinadas que apelam a certas simetrias e à rotação ou transformações geométricas em geral, e é tópico frequente das várias áreas de saber – artes e ofícios, design, desenho técnico, física e matemática, etc. Construções geométricas podem ser
modelos adequados para certos problemas, bem como podem elas mesmas constituir problemas e servir para conjecturar este ou aquele resultado ou ser subsidiárias das relações estabelecidas.
Ligados ao círculo estão sempre os polígonos inscritíveis ou circunscritíveis e os seus elementos constituintes, ângulos ao centro e inscritos, arcos e cordas, mas também o número irracional transcendente (Pi). Novos problemas de relações entre amplitudes e comprimentos, áreas ou volumes procuram resolução no quadro deste tópico de geometria. Da circunferência se podem levantar cones ou se pode introduzir o estudo dos cilindro e esfera.

2 Competências Visadas

Neste módulo de Geometria, “Geometria do Círculo”, as competências matemáticas visadas incluem os seguintes aspectos:
- a aptidão para visualizar e descrever propriedades e relações geométricas, através da análise e comparação, para fazer conjecturas e justificar os seus raciocínios;
- a sensibilidade para apreciar a geometria no mundo real, reconhecer e utilizar ideias geométricas em diversas situações e na comunicação;
- a aptidão para apreciar o papel da circunferência nos seus diversos usos com identificação das propriedades respectivas;
- a aptidão para resolver problemas através de construções, nomeadamente envolvendo  lugares geométricos, relações entre ângulos, arcos e cordas;
- a aptidão para resolver problemas envolvendo amplitudes de ângulos, comprimentos de arcos e cordas, áreas de sectores e coroas circulares ou volumes de cones e cilindros;
- a aptidão para formular argumentos válidos recorrendo à visualização e ao raciocínio geométrico, explicitando-os em linguagem corrente;
- a aptidão para reconhecer e analisar propriedades de figuras geométricas e de sólidos de revolução, nomeadamente recorrendo a materiais manipuláveis e à tecnologia.

3 Objectivos de Aprendizagem

Neste módulo de Geometria, “Geometria do Círculo”, os objectivos de aprendizagem que se pretende que os estudantes atinjam são os seguintes:
- identificar as vantagens e reconhecer a importância do uso de figuras envolvendo o círculo na resolução de problemas que envolvam comprimentos, áreas ou volumes de certas figuras planas e certos sólidos;
- mobilizar resultados matemáticos básicos necessários apropriados para simplificar o trabalho na resolução de problemas e actividades de investigação;
- conjecturar e reconhecer relações entre elementos no círculo, em círculos iguais ou diferentes, bem como entre respectivos comprimentos de arcos e de cordas, amplitudes de ângulos (e arcos);
- realizar construções como solução de problemas de geometria ou em contextos da vida quotidiana ou de outras disciplinas de saber e interpretação da realidade;
- construir modelos ou maquetas para problemas que dependam de círculos e polígonos (inscritíveis), realizando todos os cálculos necessários para dar resposta a uma encomenda de um objecto escultórico, embalagem ou de outro tipo;
- comunicar, oralmente e por escrito, aspectos dos processos de trabalho e crítica dos resultados.

4 Conteúdos
1. O círculo: perímetro e área. Ângulos ao centro e rotações. Amplitudes e comprimentos.
2. Referência a sólidos de revolução
3. Ângulos inscritos. Polígonos inscritíveis.

Circulo

Na Matemática e na Geometria, um círculo ou disco é o conjunto dos pontos internos de uma circunferência. Por vezes, também se chama círculo ao conjunto de pontos cuja distância ao centro é menor ou igual a um dado valor (ao qual chamamos raio). A área A de um círculo pode ser expressa matematicamente por:

onde r é o raio da circunferência e (Pi) uma constante.

Circunferencia

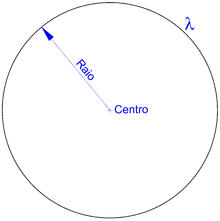
Na geometria euclidiana, uma circunferência é o lugar geométrico dos pontos de um plano que equidistam de um ponto fixo. O ponto fixo é o centro e a equidistância o raio da circunferência.

Arco de circunferencia

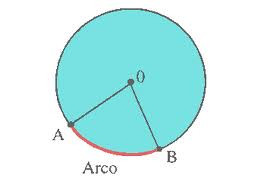
Em matemática, arco é a porção compreendida entre dois pontos (os extremos) de uma curva. Existem, por exemplo, o arco de circunferência (também chamado de arco de círculo), o arco de elipse, etc. O arco que corresponde à metade de uma circunferência é uma semicircunferência; a quarta parte é um quadrante.

Ângulo ao centro

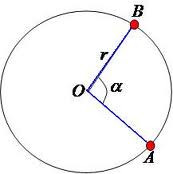
Em matemática, arco é a porção compreendida entre dois pontos (os extremos) de uma curva. Existem, por exemplo, o arco de circunferência (também chamado de arco de círculo), o arco de elipse, etc. O arco que corresponde à metade de uma circunferência é uma semicircunferência; a quarta parte é um quadrante.